Introduction 

This research aims to test theories of the liquid state, understand intermolecular interactions, and predict solvent behavior. However, physico-chemical properties such as excess functions depend upon various factors between like and unlike molecules. Here, we focus on measuring density, viscosity, and refractive index for selected systems [1-3]. The binary and ternary mixtures have been analyzed using Redlich-Kister and Cibulka relations, respectively [4,5]. Additionally, the experimental results for the ternary system fit the Tsao-Smith, Radjkovic, and Kohler models. These findings aim to contribute to the knowledge of thermodynamic properties in mixtures, which can ultimately aid in engineering design and operations.

Experimental
Chemicals

Dimethylcetamide (99.5), dimethyl-benzylamine (99) and dichloromethane (99.5) were purchased from Merck. The purity was confirmed through GC, and their density and refractive index were compared to the literature data presented in Table 1 [6,7]. The chemicals were stored in opaque containers and were purified through fractional distillation before use.
Apparatus and Procedure
Density was taken using an Anton Parr DMA 4500 densimeter in static mode, with an estimated uncertainty of ±1 × 10-5 g.cm-3. Refractive indices were measured using an Abbe refractometer with an uncertainty of ±4 × 10-5. Dynamic viscosities at 298.15 K were measured using an Ubbelohde viscometer, with an uncertainty of ±10-3 mPa.s, and viscosity was expressed as [8]:
   (1)
where k and c are viscometer parameters, and t is the time for flow. 

Table 1. Comparison of Measured DensitiesViscosities and Refractive Indices of the pure Components with Literature Values at 298.15 K
a Ref [6] b Ref [7]
Standard uncertainties u are: u (T) = 0.01 K, u (P) = 0.05 MPa, and expanded uncertainties U are: U ( ) = 3 10 -4 g•cm-3, U () = 0.02  (mPa.s)   and U (nD) = 3 10 -5 with 0.95 level of confidence.

 
Results and discussion

The  , calculated as follows:
      (2) 
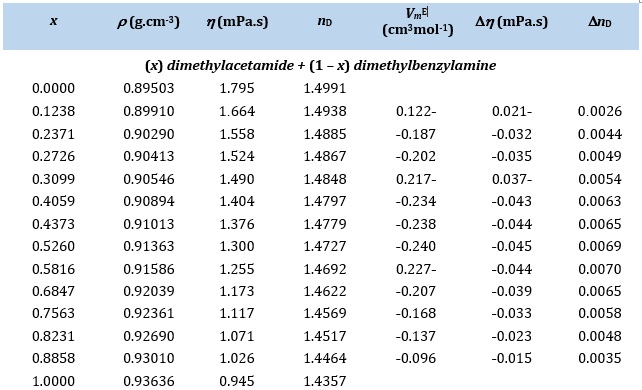
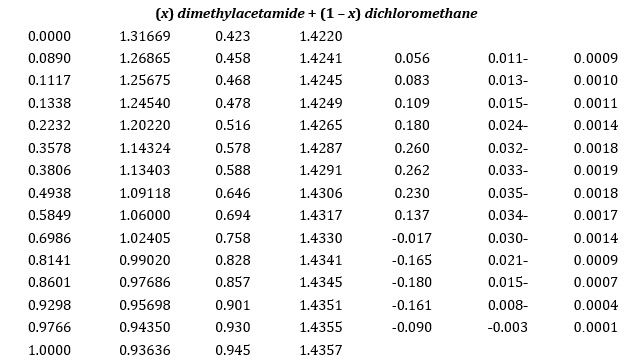
where   and Mi are density and molar mass, respectively. The resulting values of   for dimethylacetamide and dimethylbenzylamine demonstrated negative values throughout the range of mole fractions, while for dimethylacetamide + dichloromethane and dimethylbenzylamine + dichloromethane showed a sign inversion in   over part of the concentration range (x 0.65). Figure 1 displays   and density and   values have been presented (Table 2). The occurrence of favorable bipolar-bipolar intermolecular potential between unlike molecules due to their polarity is suggested to explain this observation. Additionally, the presence of alkyl groups with a positive inductive effect causes further intensification of this polarity since the negative charge congregates on the electronegative atoms. Consequently, there is a significant reduction in volume in this system. For the dimethyl acetamide + dichloromethane and dimethylbenzylamine + dichloromethane systems, a sign change from positive to negative in the zones (x 0.65) occurred. This is because at higher concentrations of amide and amine, the molecules form cages, and dichloromethane molecules occupy the spaces between these molecules, leading to a contraction in volume. However, at high concentrations of dichloromethane, undesirable interactions between dissimilar molecules lead to a positive deviation from the ideal state. 
The viscosity deviations,   was calculated using equation (3) [9]:
    (3)
where   and i are the viscosity of the mixture and pure components, respectively. Table 2 lists  and ∆ in binary systems and graphically showed in Figure 2. The results indicate that all systems exhibit negative ∆ values, with parabolic curves and the highest value observed within the x 0.5 zone. Negative ∆ values suggest that factors such as molecular size, shape, and spatial formation are also effective in addition to force and specific interactions among molecules. For instance, in the dimethylacetamide + dimethylbenzylamine system, the alkyl group and benzenoid loop's difference in shape and size leads to spatial inhibition, rendering the molecules unable to approach each other closely. As a result, the solution has a lower viscosity than each pure ingredient, resulting in negative viscosity deviation.
 

 Figure 1. Variation of excess molar volume   with mole fraction x1 for the binary systems at T = 298.15K: dimethylacetamide + dimethylbenzylamine;  dimethyl acetamide + dichloromethane ;  dimethylbenzylamine + dichloromethane. Solid curves were calculated from the Redlich–Kister equation

 Figure 2. Variation of deviation in the viscosity  with mole fraction x1 for the binary systems at T = 298.15K: dimethylacetamide + dimethylbenzylamine;  -dimethylacetamide + dichloromethane ;  dimethylbenzylamine + dichloromethane. Solid curves were calculated from the Redlich–Kister equation

Table 2. Experimental Densities , Viscosities  ,Refractive Indices nD , Excess Molar Volumes  , Deviation in the Viscosity , and Deviation in the Refractive Index nD for the Binary Systems at 298.15 K

Equation (4) defines the deviation in refractive index,   [10]:
      (4)
where   and   are the refractive index of mixtures and pure components, respectively. Across all composition ranges studied   was positive. Figure 3 displays   vs. mole fractions, and results are given in Table 2. In the case of the dimethylacetamide + dimethylbenzylamine system, the positive deviation in refractive index can be attributed to stronger bipolar-bipolar interactions between molecules, given the strong polarity of both molecules. These interactions result in increased electron density in the mixture, causing a decrease in the speed of light passing through and increasing the refractive index. 
The increase in light speed in solutions with lower viscosity results in the positive deviation observed in the refractive index.
The    and   calculated using the Redlich-Kister polynomial function to correlate data. 
    (5)
where Qij shows to  ,  or     is an parameter and   as standard deviation calculated as:
   (6)
where Qiexp and  Qical refer to the experimental and calculated value. n and p are the numbers of experimental points and several adjustable coefficients. Table 3 presents the values of the parameters   together with the standard deviation . 
Densities, viscosities, refractive indices, excess molar volumes, deviations in viscosity, and refractive index for ternary mixtures of system dimethylacetamide + dimethylbenzylamine + dichloromethane are presented in Table 4. The    and   for the ternary system were correlated using the Cibulka equation (7):
       (7)
and 
       (8)
where   refers to    and   for ternary mixtures.   in equation (8) is the binary contribution of each i-j pair to the    and   given by Equation 5 with the parameters shown in Table 3. The ternary contribution term  was correlated as:
        (9)
The ternary parameters     and  were extracted, and their values with standard deviations were given in Table 3. 
The experimental results for  , of ternary system fitted to models such as Radjkovic [11], TSAO–Smith [12], and Kohler [13].
The Radjkovic model is defined as:
    (10)    

       (11)
A12, A13 and   values are the adjustable parameters in binary systems.
The Tsao–Smith model is defined as:
      (12)
The Kohler model is given by:
             (13)
 

 Figure 3. Variation of deviation in the refractive index   with mole fraction x1 for the binary systems at T = 298.15K: dimethylacetamide + dimethylbenzylamine;  dimethylacetamide + dichloromethane ;  dimethylbenzylamine + dichloromethane. Solid curves were calculated from the Redlich–Kister equation

Table 3. Binary Coefficients of the Redlich–Kister Equation at 298.15K and Ternary Coefficients of the Cibulka Equation for  , , and nD at 298.15 K

Table 4. Experimental Densities , Viscosities  ,Refractive Indices nD , Excess Molar Volumes  , Deviation in the Viscosity , and Deviation in the Refractive Index nD for the Ternary System of Dimethylacetamide Dimethylbenzylamine and Dichloromethane at 298.15 K

Conclusion

Density, viscosity, and refractive index measurements were experimentally conducted for systems of dimethylacetamide, dimethylbenzylamine, and dichloromethane. Results showed that some solutions exhibited positive values for  , while others showed negative values. The strong bipolar-bipolar interactions between the molecules of dimethylacetamide + dimethylbenzylamine system resulted in a negative deviation, whereas undesirable interactions between dissimilar molecules in the dimethylacetamide + dichloromethane and dimethylbenzylamined + dichloromethane systems led to a positive deviation. The behavior of the solution was the result of these mutual effects. Negative values for viscosity deviation   indicated that factors such as molecular size, the shape of the ingredients, and spatial formation of molecules, in addition to the existence of forces and specific interactions among the mixture's ingredients, were also important. Shape and size of the ingredients of the alkyl group and benzenoid loop caused spatial inhibition, preventing the molecules from becoming closer to each other. As a result, the solution had a lower viscosity than each of the pure ingredients, leading to a negative viscosity deviation. Furthermore, the deviation values for the refractive index in all mole fractions were positive, with negative Δη values confirming this observation.

Acknowledgment

The authors would like to thank Bu–Ali Sina University for providing financial support for conducting this study

Disclosure statement

The authors declare that they have no conflict of interest.

Orcid 
Hossein Iloukhani  : 0000-0002-9097-7485 

HOW TO CITE THIS ARTICLE

Pegah Paran, Hossein Iloukhani*, Khatereh Khanlarzadeh. Densities, Viscosities and Refractive Indices for Binary and Ternary Mixtures of Dimethylacetamide + Dimethylbenzylamine + Dichloromethane. Adv. J. Chem. A, 2023, 6(3), 324-333. 

DOI: 10.22034/AJCA.2023.395300.1366

URL: https://www.ajchem-a.com/article_175476.html