Introduction

Deuterium, an isotope of hydrogen, exerts a notable impact on molecules due to its increased mass compared to protium, the more common hydrogen isotope. This isotopic substitution changes molecular properties and reactivity [1]. Deuterium causes a redshift in vibrational frequencies and alters reaction rates through kinetic isotope effects and hydrogen bonding behavior [2]. Deuterium labeling is widely used in research to study molecular pathways, interactions, and mechanisms [3]. Deuterium's distinctive presence has enabled its detection through spectroscopic analysis, providing a window into the conditions of interstellar regions, star formation processes, and the origin of planets [4].

In astrophysics, deuterated molecules provide valuable insights into interstellar chemistry, while in astrobiology, they offer clues about potential extraterrestrial life [5]. The presence of deuterium in molecules significantly shapes our understanding of molecular behavior, from fundamental chemical processes to its role in the interstellar medium.

Deuterium fractionation is a well-known mechanism in the thick interstellar medium that may occur both in the gas phase and on the surfaces of dust particles [6,7]. Due to this mechanism, the deuterated isotopic interstellar molecular species can have abundances much greater than the D/H elemental abundance ratio [8]. As with HDCS [9] and CH₂DOH, the great efficiency of deuterium fractionation allows deuterated species to gain 30-40% of their parent species' abundance [10]. As a result, deuterated isotopologues of a wide range of interstellar compounds considerably boost the spectrum variety. Hence, it is crucial to identify these isotopologues using astronomy to learn more about their molecular creation processes and how deuterium fractionation works and assign unidentified features in line surveys [6].

Studying isotopic abundance variations in diverse settings is an essential aspect of astrochemistry. Deuterium stands out among the visible isotopes since it is the most common rare isotope of all the elements' isotopic forms. Because the reservoir is considered primordial, astronomers are perplexed by the astral generation of tiny deuterium atoms [11]. The significant relative mass differential between hydrogen and deuterium causes the two species' distinct chemical sensitivities. This has the unintended consequence of considerably fractionating deuterium in cold clouds, where its concentration can reach three orders of magnitude higher than hydrogen. As a result, molecules with isotopically substituted deuterium atoms are easily identified. A modest number of observations of a molecule in different isotopic states enables a unique assessment of its astrochemistry [12].

Snell and Wootten (1979) revealed that the DNC/HNC abundance ratio is significantly temperature dependent. The bulk of molecular ions are destroyed due to electron recombination. Previously, it was thought that this predominated H₃⁺ destruction, allowing limits on electron abundance to be established based on estimations of the H₂D⁺/H₃⁺ abundance ratio obtained from DCO⁺/HCO⁺ abundant ratios [13,14].

The isotopic abundance of hydrogen and its isotopes varies in different environments [15]. For instance, the isotopic composition of hydrogen in water can provide insights into the sources and history of water samples. Additionally, the relative abundances of hydrogen isotopes in certain molecules can help scientists trace chemical reactions, investigate metabolic pathways, and study ancient climates by analyzing ice cores [16]

Computational Methods

The molecular geometries of SCH₂, H₂, and H₂O were optimized for all the deuterated species using the mentioned methods: MP2/cc-pVDZ, MP2/6-311*, G4, W2U, and CCSD/cc-pVDZ. The optimization process involved finding the most stable arrangements of atoms by minimizing the potential energy. Subsequently, using the same methods, frequency calculations were carried out to obtain vibrational frequencies and rotational constants for each deuterated molecule. The vibrational frequencies provided insights into the molecular vibrations, while the rotational constants described the rotational motion of the molecules. Bond lengths and angles were also computed from the optimized molecular geometries to understand the molecular structure and bonding patterns. Finally, dipole moments were computed to analyze molecules' polarity and charge distribution. The CCSD/cc-pVDZ method refers to the Coupled-Cluster Singles and Doubles calculation using the correlation-consistent polarized valence double-zeta basis set [17], which is a quantum chemical approach for accurately modeling electronic interactions in molecules. MP2/cc-pVDZ signifies the Second-Order Møller-Plesset Perturbation Theory calculation with the same basis set, an approximate post-Hartree-Fock method capturing electron correlation effects [18]. MP2-6-311* represents the MP2 method augmented with a more significant 6-311G(d,p) basis set, incorporating more basis functions for improved accuracy [19]. W2U denotes the "W2U" composite method, a combination of explicitly correlated W2-F12 and the correlation-consistent polarized valence basis set, aiming for high-precision energy calculations [20]. Lastly, G4 refers to the Gaussian-4 method, a composite approach integrating density functional theory, MP2, and CCSD(T) methods with the cc-pVnZ basis sets to achieve highly accurate thermochemical properties predictions for molecules [21]. Using the Moller-Plesset second-order perturbation theory approach (MP2), the 6-311* basis set and the correlation-consistent Polarized Valence Double Zeta (CC-Pvdz) basis set were used. In addition to the approaches described above, the coupled cluster approach was used at the correlation-consistent Polarized Valence Double Zeta (CC-Pvdz) basis set [11]. To predict suitable proton affinities for all of the systems tested, compound models such as the Gaussian theory (G4) and the Weizmann theory (W2U) were used [22,23]. All the results obtained from the above methods were compared with their experimental values obtained from the NIST Chemistry Webbook.

Results and discussion

Deuterium fractionation in the dense interstellar medium has long captivated the attention of astrophysicists and chemists alike, as it plays a pivotal role in enhancing the abundance of deuterated isotopic interstellar molecular species beyond the D/H elemental abundance ratio. This research extensively investigates deuterated molecules, explicitly focusing on H₂, H₂O, and SCH₂, employing advanced quantum chemical methods. The deuterium isotopologues of these species hold significant implications in various scientific fields, including atmospheric chemistry, combustion processes, and astrochemistry.

Hydrogen H₂

Structural Parameters

Figure 1. Optimized geometries of H₂, DH and D₂.

Table 1. Bond length values of H_2, DH and D₂

Rotational constant values for H₂, DH and D₂

The rotational constants for H₂, DH, and D₂ are 1824.327 GHz, 1368.702 GHz, and 912.676 GHz, respectively. The rotational constant of a diatomic molecule is inversely proportional to its moment of inertia, which, in turn, depends on the reduced mass of the molecule. In this case, H₂ has the highest rotational constant, followed by DH and D₂. This is because the reduced mass of H₂ is the smallest among the three, resulting in a higher rotational constant. DH, with a slightly heavier reduced mass than H₂, exhibits an intermediate rotational constant. D₂, the heaviest with the most enormous reduced mass, shows the lowest rotational constant. Thus, the comparison demonstrates that the rotational behavior of these molecules is influenced by the masses of their constituent atoms, with lighter isotopes yielding higher rotational constants.

Table 2. Rotational constants of H₂, DH and D₂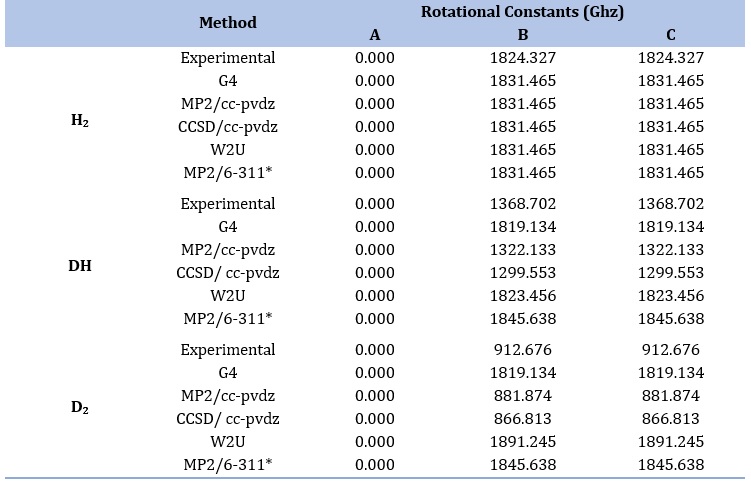

Dipole moment

Due to their linear and symmetrical molecular structures, H₂, DH, and D₂ have no dipole moment. In H₂ (hydrogen gas), the two hydrogen atoms are connected by a covalent bond, forming a linear molecule. Since both hydrogen atoms are identical and have the same electronegativity, the electron density is evenly distributed, resulting in a symmetrical charge distribution and canceling any dipole moment. Similarly, in deuterium-hydrogen (DH) and deuterium gas (D₂), the linear arrangement of the atoms and the identical electronegativity of hydrogen and deuterium lead to a symmetrical charge distribution and no net dipole moment. These molecules' positive and negative charges are perfectly balanced, resulting in a zero dipole moment, making them nonpolar.

Vibrational Frequencies

The vibrational frequencies given off by H₂, DH, and D₂ are 4161.2 cm^-1, 3632 cm^-1, and 2993.0 cm^-1, respectively. These frequencies correspond to the stretching and bending motions of each molecule's hydrogen-hydrogen (H-H) bonds. The decrease in frequency from H₂ to D can be attributed to the difference in masses; deuterium (D) is twice as heavy as hydrogen (H), resulting in a lower vibrational frequency due to a higher reduced mass. Similarly, DH, with an intermediate mass between H₂ and D₂, exhibits a frequency between the other two. This comparison illustrates the inverse relationship between vibrational frequencies and the masses of the atoms involved, highlighting how isotopic substitutions affect molecular vibrations.

Table 3. Dipole Moment values for H₂, DH and D₂

Table 4. Vibrational Frequency values of H_2, DH and D₂

Water H₂O

Structural Parameters

H₂O, HDO, and D₂O have similar bond lengths and bond angles despite having different isotopes of hydrogen (H and D) because the electronic structure of oxygen primarily governs the bonding in water molecules. The bond length and bond angle in a water molecule are mainly determined by the arrangement of its electrons and the hybridization of the oxygen atom's orbitals. Oxygen has six valence electrons, and in a water molecule, it forms two sigma bonds with the two hydrogen atoms. The electronic configuration and hybridization of oxygen remain nearly the same regardless of whether the hydrogen atoms are H, D, or a combination of both.

Since the electronic structure of oxygen remains constant, the bonding orbitals and bond angles in H₂O, HDO, and D₂O are nearly identical. As a result, the bond lengths are very similar (0.958 Å for H₂O, 0.956 Å for HDO, and 0.956 Å for D₂O) because the spatial arrangement of the atoms is not significantly affected by the substitution of hydrogen with deuterium. The slight difference in bond lengths can be attributed to subtle changes in the atomic masses. However, overall, the similarity in the bond angles and lengths is primarily due to the consistent electronic configuration and hybridization of the oxygen atom in all three water isotopologues.

Figure 2. Optimized geometries of H₂O, DHO and D₂O

Table 5. Bond Lengths and Bond Angles of H₂O, DHO and D₂O 

 Rotational Constants

The rotational constants of H₂O, HDO, and D₂O differ due to the isotopic substitutions of hydrogen with deuterium. The rotational constant of a diatomic molecule is inversely proportional to its moment of inertia, which, in turn, depends on the reduced mass of the molecule. When deuterium replaces hydrogen, the molecular mass increases, resulting in a higher reduced mass for HDO and D₂O compared to H₂O. Consequently, the moment of inertia increases for HDO and D₂O, leading to lower rotational constants. Thus, H₂O, the lightest isotopologue, has the highest rotational constants (835.73144 GHz, 435.05882 GHz, and 278.35730 GHz for the three rotational axes). In comparison, the rotational constants decrease for HDO (701.93 GHz, 272.90 GHz, and 192.06 GHz) and further decrease for D₂O (462.279 GHz, 218.038 GHz, and 145.258 GHz) due to the increasing masses of deuterium, highlighting the impact of isotopic substitutions on the rotational behavior of these water isotopologues.

Table 6. Rotational constant values for H₂O, HDO, and D₂O

Dipole Moments

The dipole moments of H₂O, HDO, and D₂O are 1.860 Debye, 1.850 Debye, and 1.850 Debye, respectively. The molecular geometry and electron density distribution within these water isotopologues can explain the similarity in their dipole moments. In all three molecules, the central oxygen atom is highly electronegative, causing it to attract the shared electrons in the O-H bond toward itself. This creates a significant partial negative charge on the oxygen atom and a partial positive charge on the hydrogen or deuterium atoms.

The dipole moment of a molecule is the product of the charge and the distance between the charges, so even though HDO and D2O have heavier isotopes (deuterium) compared to H₂O (hydrogen), the difference in dipole moments is minimal because the change in charge distribution upon isotopic substitution is relatively tiny. The geometry of the water molecule, with the oxygen atom at the center and the hydrogen/deuterium atoms forming a bent shape, leads to a comparable arrangement of the partial charges in H₂O, HDO, and D₂O. As a result, their dipole moments are similar despite the isotopic differences, making them all highly polar molecules with only marginal variation in their overall polarity.

Vibrational Frequency

The vibrational frequencies of H₂O, DHO, and D₂O exhibit interesting patterns due to the isotopic substitutions of hydrogen with deuterium. These frequencies represent the energies required for the molecules to undergo different vibrational modes, such as stretching and bending motions. When comparing the vibrational frequencies, several trends become apparent.

The vibrational frequencies of H₂O, DHO and D₂O can be seen in the table below. For H₂O, the vibrational frequencies are 3657.0 cm^-1 (stretching), 1595.0 cm^-1 (bending, in-plane), and 3756.0 cm^-1 (bending, out-of-plane). As we move to DHO, which contains one deuterium (D) and one hydrogen (H), the vibrational frequencies shift to 3707.0 cm^-1 (stretching), 2727.0 cm^-1 (bending, in-plane), and 1402.0 cm^-1 (bending, out-of-plane). Notably, DHO has higher vibrational frequencies compared to H₂O, particularly for the stretching and bending in-plane modes. Finally, D₂O, with both hydrogens replaced by deuterium, shows vibrational frequencies of 2671.0 cm^-1 (stretching), 1178.0 cm^-1 (bending, in-plane), and 2788.0 cm^-1 (bending, out-of-plane). D₂O exhibits the lowest vibrational frequencies among the three isotopologues, as the heavier deuterium atoms result in higher reduced masses, leading to a decrease in vibrational energies.

In summary, the isotopic substitutions influence the vibrational frequencies of H₂O, DHO, and D2O. The presence of deuterium atoms leads to lower vibrational frequencies due to the increased molecular mass, which affects the reduced mass and alters the energy requirements for molecular vibrations. Additionally, the stretching and in-plane bending modes are more sensitive to isotopic substitutions, resulting in more pronounced shifts in their vibrational frequencies compared to the out-of-plane bending mode. Understanding these variations in vibrational frequencies provides valuable insights into the isotopic effects on molecular behavior and has implications in various fields, including spectroscopy, astrochemistry, and environmental studies.

Table 7. Dipole Moment values for H₂O, HDO and D₂O

Table 8. Vibrational Frequency values for H₂O, HDO and D₂O

Structural Parameters 

Table 9. Bond length values for SCH2, SCHD and SCD2

Table 10. Bond angle values for SCH2, SCHD and SCD2

Rotational Constant

The rotational constants of SCH₂, SCDH, and SCD₂ exhibit clear trends due to isotopic substitutions, which significantly impact the molecular rotational behavior. Rotational constants measure the moment of inertia of a molecule, and they depend on the masses of the atoms involved. By examining the provided data, we can observe distinct patterns in the rotational constants and understand the reasons behind these trends.

The first paragraph describes the trend as follows: The rotational constants decrease as we move from SCH₂ to SCDH and then to SCD₂. In SCH₂, the rotational constants are 291.614 GHz, 17.700 GHz, and 16.652 GHz. As sulfur (S) forms polar covalent bonds with carbon (C) and hydrogen (H), the molecule's rotational behavior is influenced by its geometry and mass distribution. With replacing one hydrogen by deuterium (D) in SCDH, the rotational constants decrease to 197.918 GHz, 16.218 GHz, and 14.9900 GHz. The higher mass of deuterium leads to a more substantial decrease in the rotational constants as the rotational motion becomes more restricted. Finally, in SCD2, with both hydrogens replaced by deuterium, the rotational constants drop further to 142.697 GHz, 14.977 GHz, and 13.554 GHz. The increased mass of deuterium significantly affects the moment of inertia, resulting in lower rotational constant values along all three axes. Their rotational constants can be seen in the table below.

In the second paragraph, the reasons for the observed trend can be discussed: The trend in the rotational constants can be attributed to the changes in molecular mass due to isotopic substitutions. Deuterium (D) is heavier than hydrogen (H), and its inclusion in the molecules decreases the rotational constants due to the higher reduced moment of inertia. As the molecular mass increases, the rotational motion becomes more restricted, leading to lower rotational constant magnitudes. Additionally, molecular geometry plays a role in determining the rotational constants. In SCH₂, the rotational constants are higher due to the contributions from the lighter hydrogen atoms. However, with isotopic substitutions, the rotational constants decrease as the heavier deuterium atoms alter the mass distribution and the moment of inertia. The trends in rotational constants provide valuable insights into how isotopic substitutions affect the rotational behavior of molecules, and they offer essential information for understanding molecular structure and dynamics.

Dipole Moment

In the case of SCH₂, the presence of a sulfur (S) atom bonded to a carbon (C) atom and two hydrogen (H) atoms results in a bent molecular geometry. The sulfur-carbon (S-C) bond and sulfur-hydrogen (S-H) bonds have different electronegativities, creating a polarity along these bonds. This leads to an overall dipole moment for the molecule. A dipole moment of 1.761 Debye for SCH₂ indicates that the molecule has a moderate level of polarity. The specific value of the dipole moment depends on the geometry and charge distribution within the molecule.

The dipole moment of SCH₂ is a crucial parameter for understanding its reactivity, solubility, and interactions with other molecules. It plays a significant role in determining the molecule's behavior in chemical reactions and its interactions in various environments, including in solutions or in the gas phase. Knowledge of the dipole moment helps researchers predict and interpret the properties and behavior of SCH₂ and is essential for a comprehensive understanding of its molecular characteristics.

Table 11. Rotational constant values for SCH2, SCHD and SCD2

Table 12. Dipole Moment values of SCH₂, SCDH and SCD₂

Vibrational Frequency

The discrepancies observed in the vibrational frequencies of SCH₂, CSDH, and SCD₂ arise due to the isotopic substitutions and the resulting molecular mass and bond strength changes. Vibrational frequencies represent the energies required for molecular vibrations and are highly sensitive to the masses of the atoms involved in the molecule.

In SCH₂, the frequencies are 990.2 cm^-1, 991.0 cm^-1, 1059.2 cm^-1, 1455.5 cm^-1, 2971.0 cm^-1, and 3024.6 cm^-1. The presence of sulfur (S) and deuterium (D) atoms, along with carbon (C) and hydrogen (H) in SCH₂, leads to unique vibrational modes, resulting in a range of frequencies.

In CSDH, with one hydrogen atom replaced by deuterium, the frequencies are 814.4 cm^-1, 929.8 cm^-1, 1074.9 cm^-1, 1357.5 cm^-1, 2285.6 cm^-1, and 3115.9 cm^-1. The isotopic substitution alters the masses of the atoms, leading to differences in the reduced mass and bond strengths, which, in turn, affect the vibrational frequencies.

In SCD₂, with both hydrogens replaced by deuterium, the frequencies are 759.03 cm^-1, 814.21 cm^-1, 954.29 cm^-1, 1198.8 cm^-1, 2226.2 cm^-1, and 2351.3 cm^-1. The heavier deuterium atoms result in lower vibrational frequencies due to the increased reduced mass and weakened bonds.

The observed discrepancies in the vibrational frequencies among SCH₂, CSDH, and SCD₂ showcase the significant impact of isotopic substitutions on molecular vibrations. Different isotopologues have distinct masses and bond strengths and exhibit different vibrational energy requirements. These discrepancies are valuable for understanding the influence of isotopes on molecular behavior, and they hold importance in fields such as spectroscopy, environmental studies, and astrochemistry.

Table 13. Vibrational Frequency values of SCH₂, SCDH and SCD₂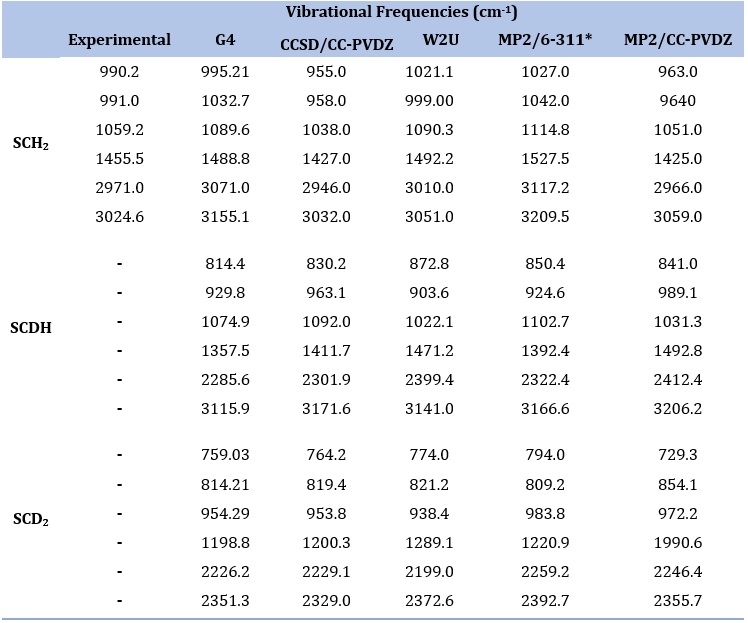

Conclusion

In conclusion, our computational methodology enabled a detailed exploration of how deuteration influences the spectroscopic properties of the studied molecules. The observed changes in dipole moments, vibrational frequencies, and rotational constants enrich our understanding of the deuteration-induced modifications in molecular behavior. Results revealed that the CCSD/cc-pVDZ method exhibited the highest level of accuracy among the computational methods employed while investigating the deuterated species. This superior accuracy is crucial for capturing electron correlation effects and yielding more reliable predictions of the molecular properties of deuterated species. By identifying CCSD/cc-pVDZ as the most accurate method, our research provides valuable benchmarks for future studies involving deuterated molecules and highlights the significance of utilizing high-level quantum chemical approaches to attain precise results. authors are grateful to the

Disclosure statement

The authors declare that they have no conflict of interest

Orcid

John Paul Shinggu : 0009-0005-2216-3155

Emmanuel Edet Etim : 0000-0001-8304-9771

HOW TO CITE THIS ARTICLE

John Paul Shinggu *, Emmanuel Edet Etim, Alfred Ikpi Onen. Isotopic Effects on the Structure and Spectroscopy of Thioformaldehyde, Dihydrogen and Water, Adv. J. Chem. A, 2023, 6(4), 366-379. 

DOI: 10.48309/AJCA.2023.409538.1389

URL: https://www.ajchem-a.com/article_178011.html