Introduction

Utilizing BNNTs as sensors for metal ions has the capacity to significantly transform numerous industries and applications through the provision of enhanced accuracy, sensitivity, and selectivity in detection capabilities [1-9]. They possess the ability to identify and measure the presence of metal ions in various environmental samples, including water and soil [10]. This can aid in the surveillance and management of pollution levels, while also guaranteeing adherence to regulatory benchmarks. BNNTs can be utilized for detecting metal ions in biological samples, such as blood or urine. This could potentially facilitate the early detection of disorders linked to atypical levels of metal ions, such as Wilson's disease [11,12]. These sensors can be utilized to detect metal ions in industrial operations, such as mining or manufacturing. This could enhance the streamlining of production operations and minimize both waste generation and environmental footprint [13]. They can also be employed for detecting metal ions in food samples, such as seafood or fruits and vegetables. This could aid in guaranteeing the safety and excellence of food products and in averting food contamination [14].

BNNTs have been proven to have great selectivity for certain metal ions, which indicates that they can reliably detect and distinguish between distinct metal ions even in complicated samples. They have a high level of sensitivity towards metal ions, even when present in low concentrations. This demonstrates their ability to accurately and precisely detect metal ions, a crucial aspect for numerous applications [15]. BNNTs exhibit rapid response time, indicating their ability to promptly and precisely detect fluctuations in metal ion concentrations. This is crucial for applications that necessitate instantaneous monitoring and control [16]. These entities exhibit stability and are capable of functioning effectively throughout a broad spectrum of conditions, such as elevated temperatures and environments with high acidity or alkalinity [17,18]. This renders them well-suited for deployment in demanding and hostile conditions. Ultimately, they possess a very affordable price in comparison to alternative nanotube variants, rendering them appealing for a multitude of purposes.

The choice of the (5,0) configuration of BNNT in this study is noteworthy because of its comparative simplicity and its prevalence in experimental and computational investigations [19-23]. Previous studies have demonstrated that the arrangement of BNNTs in a (5,0) configuration exhibits favorable outcomes in terms of adsorption. In one investigation [24], the adsorption of CO on the surfaces of four finite-length zigzag (5,0) nanotubes—BN, AlN, BP, and AlP nanotubes was examined theoretically. An independent investigation [25] looks at the mechanism by which the HO₂ radical sticks to a (5,0) zigzag BNNT's exterior. These findings indicate that the (5,0) zigzag model of BNNT could be a suitable choice for investigating the adsorption characteristics of different molecules and ions. The study conducted in 2021 [26] utilized first-principles computations to examine the adsorption of tiny atoms and molecules on the zigzag (5,0) and armchair (5,5) BNNTs. The findings indicate that the adsorption energies of the atoms and molecules were greater on the zigzag (5,0) BNNT compared to the armchair (5,5) BNNT.

The stability of the nanotube under investigation has been assessed by examining its total energy, electrical structure, and vibrational properties. Typically, the stability of a nanotube is influenced by its diameter. Nanotubes with reduced diameters exhibit enhanced stability due to their diminished surface energy and reduced susceptibility to structural flaws [27]. Furthermore, nanotubes that possess greater levels of symmetry, such as those with consistent diameters and chirality’s, tend to exhibit higher stability [28,29]. Symmetry facilitates the uniform distribution of stress across the nanotube structure. The stability of a nanotube can be affected by its interactions with the surrounding environment, including factors such as temperature, pressure, and exposure to gases or liquids [30]. These variables have the potential to impact both the physical strength and chemical responsiveness of the nanotube.

In the nanotubes evalusation, the absorbed wavelength related to the energy gap is also important. There is the relationship between these wavelengths with calculated band gap of doped compounds by cations [31]. For instance, in TiO₂'s photocatalytic activity, pure TiO₂ is only active when exposed to ultraviolet (UV) light (E_g = 3.2 eV), which makes it ineffective in absorbing visible light [32]. Using chemical doping, the band gap energy of TiO₂ is changed, allowing the absorption band to shift to the visible region [33,34]. Many efforts have been made to increase the sensitivity of modified TiO₂, such as doping with transition metals, nonmetal atoms, and organic materials, to enhance photocatalysis activity [35].

The interaction energy between the ions and the nanostructures has been investigated in many studies [36]. This study uses the DFT approach to examine the adsorption of metal cations (M = Cr²⁺, Mn²⁺, Fe²⁺, Cu⁺, Ag⁺, and Au⁺) on the surface of pure BNNT (M@BNNT). In this analysis, we examine the optimal parameters, adsorption energies, and density of state graphs. To assess the electronic characteristics, stability, and reactivity of cations adsorbed on the surface of nanotubes, we also examine the frontier molecular orbitals and several overall reactivity descriptors, including energy gap, chemical hardness, softness, and electronegativity. The NBO analysis is employed to determine the characteristics of bonds and the distribution of atomic charges in the systems under investigation. We anticipate that our findings will offer significant insights into the adsorption of cations utilizing BN nano-materials.

Computational details

Geometry optimization, energy calculations, and density of states analysis are performed using the quantum chemistry software Gaussian 09 [31]. The results are obtained using the ωB97XD approach [32] and the 6-31G(d,p) basis set [33]. The current method combines long-range correction with empirical atom-atom dispersion [34–36]. Therefore, it is a helpful tool when studying non-covalent complexes. Given the complete saturation of the hydrogen atoms in the BNNT structure, it could be necessary to use a 6-31G(d,p) basis set. The Ag⁺ and Au⁺ metal ions also employ the SDD standard basis set [37]. It is renowned for its precision in representing core potentials. The zigzag (5,0) BNNT that we are examining here is composed of 10 hydrogen (H), 20 boron (B), and 20 nitrogen (N) atoms. The assessment of the interaction between the cations and the pure BNNT is as follows, based on the adsorption energies (E_ads):

E_ads = E_(M@BNNT) – E_(BNNT) – E_(M) + E_BSSE                 (1)

According to the formula, the total energy of the BNNT when interacting with the cations is represented by E_(M@BNNT). The total energies of the isolated cations (E_(M)) and pure BNNT (E_(BNNT)), respectively, are indicated. The complexes are created via an exothermic process that produces a stable structure, as indicated by the negative E_ads values. Using the counterpoise correction method, which was first put forth by Boys and Bernardi [38], the adsorption energies of the complexes are modified to take the basis set superposition error (BSSE) into account. Furthermore, the interaction (E_int) and deformation (E_def) energy components add up to the adsorption energy. Consequently, it is thought that the following equations can give the exact values of these components:

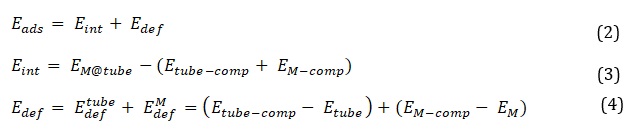
In relaxed complexes, the energies of cations and nanotubes are denoted by the symbols E_M-comp and E_tube-comp, respectively. The zero-point vibrational energies (ZPVE), which are crucial to the overall energy, are obtained through frequency calculations carried out at a consistent theoretical level. Lack of imaginary frequencies suggests that the complexes under study are stable because they have certain local minima on the potential energy surface (PES). The partial density of states (PDOS) spectra and total density of state (TDOS) curve are visualized using the software Multiwfn 3.6 [39]. These are produced with the information gathered from ωB97XD/6-31G(d,p) computations. We do the NBO analysis [40] at the same theoretical level to evaluate the charge transfer of the cations adsorbed on the BNNT.

The electronic characteristics of the examined structures are investigated utilizing frontier molecular orbitals (FMOs) such as the highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO), and their energy gap (E_g). The quantum molecular descriptors, including softness (S), global hardness (η) [41], and electronegativity (χ) [42], are further assessed. Ultimately, the molecular electrostatic potential (MEP) energy surface is computed to characterize the molecular charge distribution in the analyzed complexes.

Results and discussion

Adsorption energy and molecular geometry

The mechanism by which metal ions are drawn to pure BNNT (M@BNNT) in the gas phase is investigated in this work. The frequency computations are carried out to determine the binding energies of different complexes at 25 °C and one atmospheric pressure.

According to Figure 1, the BNNT structure in this work has a charge of 0 and a spin multiplicity

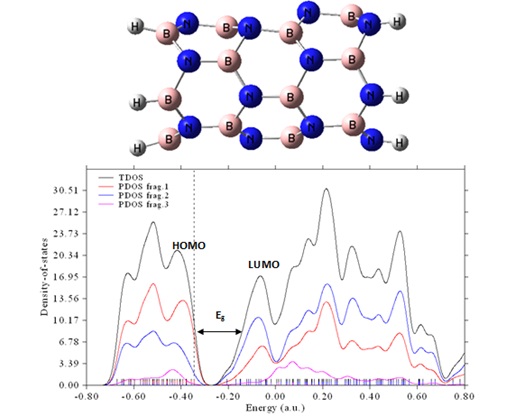
Figure 1. The optimized structure along with the Total DOS and PDOSs of atoms in the pristine BNNT (the N atoms as fragment 1, the B atoms as fragment 2, and all hydrogen as fragment 3).

of 1. The M@BNNT systems have a total charge of +1 for monovalent cations and +2 for divalent cations according to DFT calculations. The spin multiplicity of the Cr²⁺, Fe²⁺, Cu⁺, Ag⁺, and Au⁺ complexes is singlet, while the Mn²⁺ complex has a doublet spin multiplicity. To adsorb the chosen ions, we examine four potential locations on the BNNT: the B-N bridge site, the boron and nitrogen sites, and the hexagonal hollow site. The results indicate that the optimal spot for the adsorption of metal ions on the nanotube is located directly above the hexagonal hollow site. Following optimization, the monovalent ions are positioned above the nitrogen site, whereas the divalent ions are situated above the hexagonal hollow site (see Figures 2a and 3a).

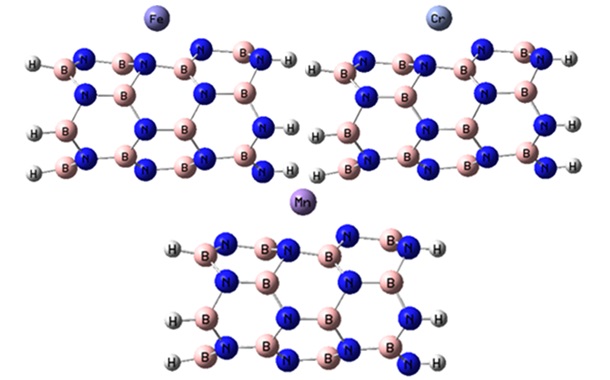
Figure 2a. The optimized structures of the M²⁺@BNNT complexes.

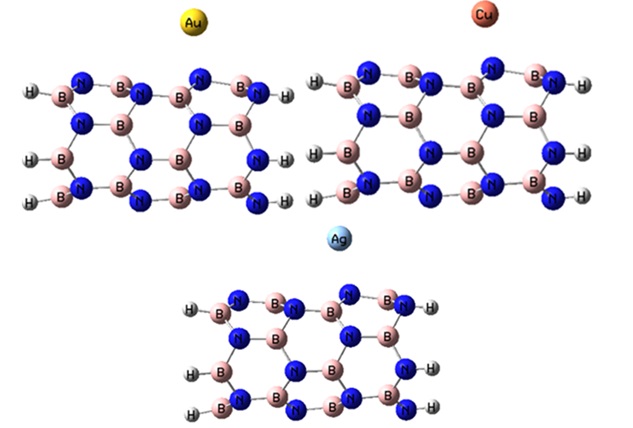
Figure 3a. The optimized structures of the M⁺@BNNT complexes.

Table 1. The adsorption energy (E_ads), interaction energy (E_int) and deformation energy (E_def) (kJ mol^-1) of cations adsorbed on pristine BNNT, and thermodynamic parameters of complex formation (ΔH, ΔG, and ΔS, in kJ.mol^-1) for different examined complexes

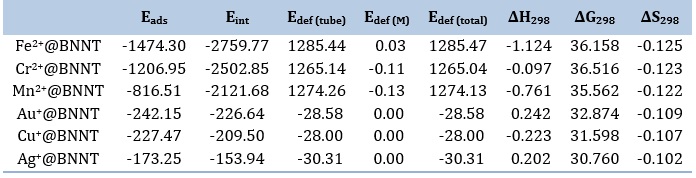
The adsorption energies that have been determined can be used to identify the most stable arrangements. The cation type and its charge density are crucial elements that impact the E_ads values.

Table 1 indicates that the monovalent ion with the highest adsorption energy is Au⁺@BNNT. The distance between the ion and the center of the ring engaged in the interaction, known as d_π…M, is 2.094 Å and the adsorption energy, denoted as E_ads, is -242.15 kJ/mol. However, Fe²⁺@BNNT is discovered to be the most stable among divalent complexes, with a d_π…M distance of 1.644 Å and an E_ads value of -1474.30 kJ/mol. The adsorption energies for the divalent complexes are significantly greater than those of the monovalent ones, indicating that the nanotube exhibits a high sensitivity to divalent cations. The observed results indicate that the adsorption of cations on the BNNT is a chemisorption process, which likely explains the ionic interaction between the species. This suggests that the pure BNNT is sensitive to metal ions and has the potential to be utilized for detecting the selected ions.

The adsorption energy can be represented as the sum of two separate components: the interaction energy and the deformation energy. The values of these two elements have been calculated for all of the analyzed systems using Equations 2-4, as listed in Table 1. After analyzing the results, it is clear that the Fe²⁺@BNNT and Au⁺@BNNT complexes demonstrate the maximum degree of interaction energy. The main factor influencing the formation of complexes is the modification in the nanotube structure that occurs during the process of cation adsorption on the BNNT surface. Therefore, the study additionally investigates the energy values related to the deformation of nanotubes after the adsorption of cations. The findings in Table 1 demonstrate that the structural characteristics of the nanotubes barely change upon adsorption. The incredibly low deformation energy values are the reason for this.

The data obtained from frequency calculations (see Table 1) are evaluated to determine thermodynamic parameters, such as the change in enthalpy (ΔH), the change in Gibbs free energy (ΔG), and the change in entropy (ΔS). The findings imply that the calculated ΔH values show negativity. Stated differently, the formation of complexes is characterized by an exothermic reaction (ΔH < 0), and the collected data suggest that the enthalpy change is beneficial. Moreover, the complexes' synthesis is thermodynamically unfavorable, as indicated by the positive ΔG value. When the calculations are examined closely, it becomes clear that ΔS is negative and that ΔH is smaller than TΔS (|ΔH| < |TΔS|). Consequently, the entropic factor controls the stability of the chosen compounds. Table 1 indicates that the BNNTs with divalent cations have larger ∆H values. With the exception of Cu⁺@BNNT,  the  analyzed  structures  thus show

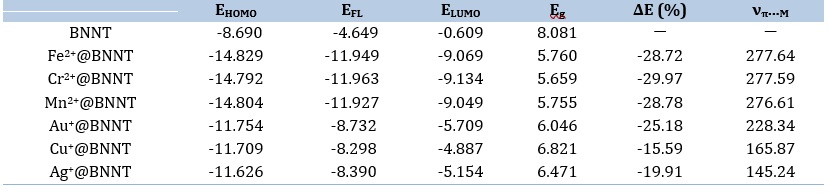
Table 2. The energies of HOMO and LUMO (E_HOMO and E_LUMO, in eV), energy of Fermi level (E_FL, in eV), energy gap (E_g, in eV), change of E_g upon adsorption of cations (ΔE (%)), and stretching frequencies of π∙∙∙ion (ν_π..._M, in cm^-1)

more adsorption processes in these complexes than in their original counterparts containing single-charged ions.

Using the 6-31G(d,p) basis set and the theory-level ωB97XD technique, the geometric parameters are optimized. There are two different kinds of B-N bonds in the isolated BNNT. One variety is parallel to the tube axis and has a bond length of 1.445 Å. The other form, shown in Fig. 1, has a bond length of 1.461 Å, but it is not parallel to the tube axis. On the other hand, the data show that the BNNT has a B–N–B angle of 107.0°, which is greater than that of its similar complexes. The B-N-B angles change to the following values after cations adsorb on the nanotube surface: Fe²⁺ (103.8°), Cr²⁺ (101.2°), Mn²⁺ (102.6°), Au⁺ (101.2°), Cu⁺ (101.2°), and Ag⁺ (101.8°).

An additional factor that is strongly linked to the strength of the intermolecular interactions is the modification of the cation-π stretching frequency.

In order to better understand the effectiveness of these interactions, we have calculated the vibrational frequencies of all the complexes. It is well acknowledged that as the interaction becomes stronger, the degree of shifting gets more pronounced. Table 2 presents the stretching frequencies (ν_π...M) of the cation–π contact (interaction) for the complexes being studied. It is crucial to emphasize that when the cation–π interactions increase in strength, their stretching frequencies shift towards higher wavenumbers, as presented in Table 2.

Electronic properties

The impact of cation adsorption on the electronic characteristics of pure BNNT is assessed through the determination of energy gap values derived from complexation. The energy gaps, which are determined by subtracting the highest occupied molecular orbital (HOMO) energy from the lowest unoccupied molecular orbital (LUMO) energy, are listed in Table 2.

Accordingly, the adsorption of metal ions on the BNNT can result in significant alterations in the electronic characteristics of the nanotube due to the observable modifications in their energy gaps. The results indicate that the measured values of E_g decrease with respect to the comparable unaltered BNNT. Table 2 demonstrates that the adsorption of divalent cations on the BNNT results in the lowest values of E_g. This is attributed to the greater electronic charge transfer of these complexes in comparison to the other complexes under consideration. Furthermore, it is evident that the percentage change in energy gap (%ΔE) in the divalent complexes is higher compared to that in the monovalent systems, indicating the nanotube's strong responsiveness to the adsorption of divalent ions.

The density of state plots for the isolated BNNT and its complexes are also computed to examine

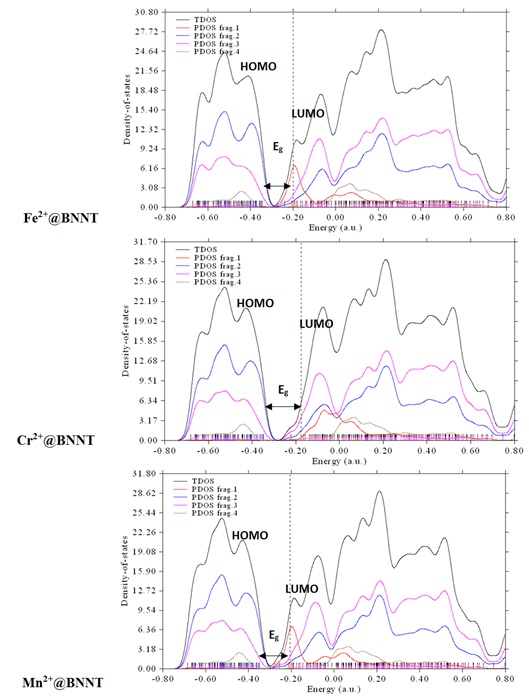
Figure 2b. The Total DOS and PDOSs of atoms involved in the interactions at the M²⁺@BNNT complexes (the Fe, Cr, and Mn cations as fragment 1, the N atoms as fragment 2, the B atoms as fragment 3, and all hydrogens as fragment 4).

the electronic structure and the susceptibility of the pristine BNNT to the chosen metal ions (see Figures 1, 2b, and 3b). The calculated DOS plots exhibit that the electronic properties of the pristine BNNT significantly change with the addition of metal cations. According to the M@BNNT DOS diagrams (Figures 2b and 3b), the E_g values of the divalent complexes considerably change and shift toward lower energies compared to those with monovalent complexes. This demonstrates the heightened sensitivity of pure BNNT to divalent cations as opposed to monovalent ones; thus, the Fermi level energy (E_FL, middle of the E_g at 0 K) for divalent cations adsorbed on nanotube would diminish from -4.649 eV in the pristine BNNT to -11.949 eV in the Fe²⁺, -11.963 in Cr²⁺, and -11.927 eV in Mn²⁺. Therefore, the evident impact of the electrical characteristics throughout the adsorption process indicates that the intrinsic BNNT is well-suited for detecting the specific metal ions in question.

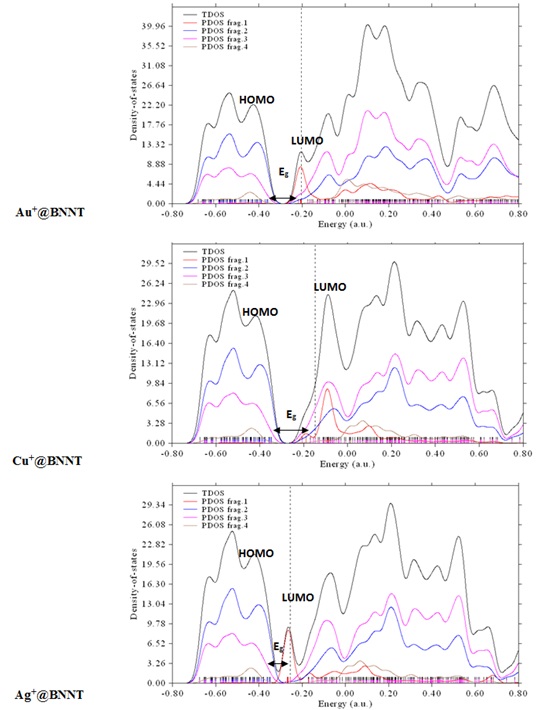
Figure 3b. The total DOS and PDOSs of atoms involved in the interactions at the M⁺@BNNT complexes (the Au, Cu, and Ag cations as fragment 1, the N atoms as fragment 2, the B atoms as fragment 3, and all hydrogen as fragment 4).

As displayed in Figure 1, every vertical line on the total density of states (TDOS) map represents a distinct molecular orbital (MO), while the dotted line indicates the precise location of the HOMO. The distribution of energy levels in the molecular orbitals determines the computed TDOS, which is represented by the graph. The partial density of states (PDOS) calculation is very useful for providing a visual representation of the orbital composition analysis. This study evaluates these compositions using the Hirshfeld technique, as mentioned in reference [39].

The larger peak value of the PDOS for the atoms of boron (B) in the BNNT suggests that these atoms can play a major role in the interaction between the nanotube and the adsorbed cations. As can be seen in Figures 1, 2b, and 3b, the PDOS curves in the generated figures exhibit a greater extent of high-energy regions, suggesting that the majority of the π MOs in these systems have higher energy levels than the σ MOs.

The E_g values also affect the conductivity of the complexes. Semiconductor material electrical conductivity is directly related to the E_g values, which can be exponentially represented with the following equation:

σ α exp (-E_g/2kT)                                                     (5)

The equation represents the relationship between σ, which denotes the electrical conductivity, and k, which represents Boltzmann's constant. At a specific temperature, it can be observed that the drop in E_g is accompanied by an increase in σ. Table 2 reveals that the decrease in E_g in the complexes containing divalent cations is more significant compared to the complexes containing monovalent cations. This results in a greater electrical conductivity of the complexes in the former situations compared to the latter.

The work function (ϕ) of a semiconductor is governed by the charge transfer between the adsorbent and the adsorbate. The Fermi energy is the minimal amount of energy needed to move an electron from the Fermi level to an away distance. The procedure for determining the work function is as follows:

ϕ = E_inf - E_FL                                                                (6)

Where, E_inf denotes the electrostatic potential at infinity, while E_FL represents the energy of the Fermi level. In this equation, the value of E_inf is expected to be zero, while the E_FL is positioned close to the midpoint of the E_g (at a temperature of 0 Kelvin). The correlation between the decrease in Fermi level energy and the increase in work function is provided in Tables 2 and 3.

The work function changes (Δϕ) are calculated by comparing the work function of pure BNNT with that of the comparable adsorbed systems. The results indicate that the values of Δϕ are positive. Furthermore, the interaction between cations and the pristine BNNT results in greater work functions following complexation, in comparison to the isolated BNNT. The observed phenomenon can be attributed to the transfer of electric charge from the tube surface to the cations. This transfer is accompanied by an increase in the conductivity of the nanotube during the process of complexation. Table 3 demonstrates that the significance of these results is greater in the divalent ions compared to the monovalent ones.

The adsorption process causes a modification in the work function of the isolated BNNT, resulting in a corresponding alteration in its field emission properties. The electron current density emitted in vacuum (J) is exponentially related to the negative value of the work function.

J = AT² exp (-ϕ/kT)                                                 (7)

Where, T is the temperature in Kelvin (K), k is the Boltzmann constant, and A is the Richardson constant expressed in square meters (m²). It should be noted that there is a correlation between a drop in the emitted current density and an increase in the work function. In addition, the data show that the electron current density emitted during the complexation process is significantly lower when divalent cations are adsorbed than when monovalent cations are. This implies that evaluating the field emission characteristics might be more dependent on the divalent ions' capacity to stick to the pure BNNT.

The molecular dipole moment (μ°) is an electrical property that has an impact on the specified structures. This experimental test provides a straightforward assessment of the charge distribution in a molecule, with its direction determined by the locations of positive and negative charges.

Table 3 summarizes the dipole moment values obtained at the ωB97XD/6-31G(d,p) level of theory. The dipole moment of the isolated BNNT is 6.26 D, as the table demonstrates. The dipole moment values rise and the dipole moment vector's direction shifts as cations adsorb onto the nanotube surface. The charges migration from one portion of the molecule to another and the redistribution of electric charges brought on by interactions between different species may be the source of this occurrence [43]. The biggest and lowest dipole moment values, respectively, are found in the Cr²⁺ and Au⁺ cations adsorbed on the nanotube, according to the findings.

Frontier molecular orbital (FMO) analysis

Our objective in this part is to examine the reactivity of BNNT by examining its electronic structure. The HOMO and LUMO diagrams of the isolated BNNT and its complexes are depicted in Figures 4a-4c. According to the observation in Figure 4a, the HOMO and LUMO levels are predominantly located on the nitrogen (N) and boron (B) atoms, respectively. This indicates that the N atoms possess an abundance of electrons, while the B atoms have a deficiency of electrons. Figures 4b and 4c display the molecular orbital diagrams of the HOMO and LUMO on the BNNTs loaded with cations. The investigation focuses on the most stable configurations, Fe²⁺@BNNT and Au⁺@BNNT, which were computed using the ωB97XD/6-31G(d,p) level of theory. The HOMO orbital of Fe²⁺@BNNT is situated on the Fe²⁺ cation and the ring engaged in the interaction, whereas the LUMO is predominantly found on the surface of BNNT. The HOMO and LUMO diagrams of the Au⁺@BNNT complex exhibit reversed observations.

Table 3 summarizes the global reactivity descriptors, namely chemical hardness (η), softness (S), and electronegativity (χ). The kinetic stability and chemical reactivity of compounds can be determined using the equations derived from Koopman's theorem [44]. The quantities are calculated as follow:

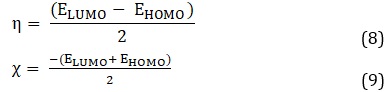
E_LUMO and E_HOMO are the energy levels of the lowest unoccupied molecular orbital and the highest occupied molecular orbital, respectively. The softness is represented by the reciprocal of the hardness, as follow:

Table 3. The work function and its changes (ϕ and Δϕ, in eV), electronegativity (χ, in eV), hardness (η, in eV), softness (S, in eV^-1), number of electrons transferred (ΔN), and dipole moment (μ°, in Debye)

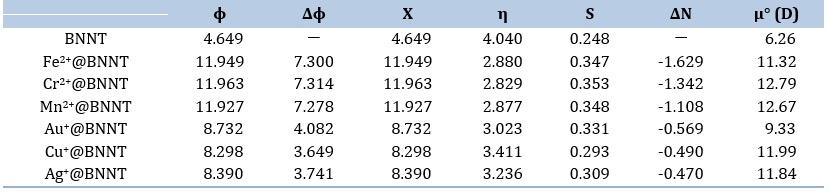
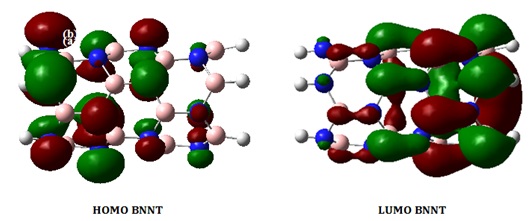
Figure 4a. Molecular orbitals of the HOMO and LUMO for the isolated BNNT at the ωB97XD/6-31G(d,p) level of theory

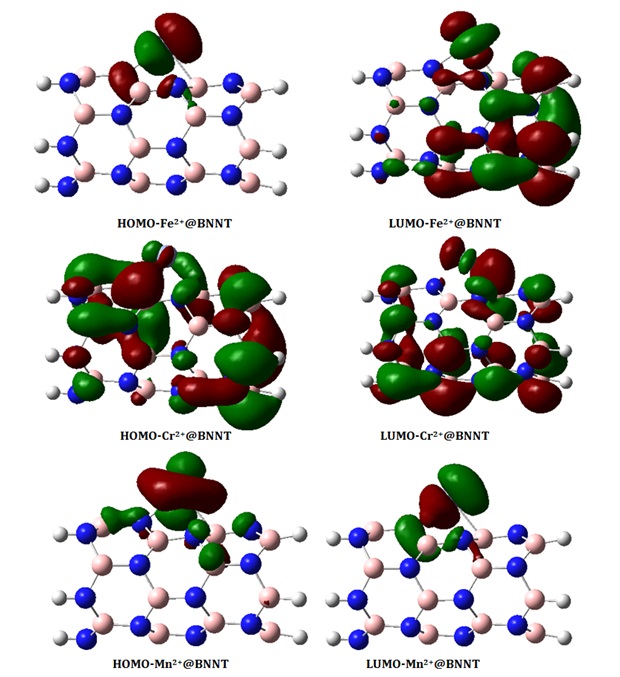
Figure 4b. Molecular orbitals of the HOMO and LUMO on the BNNTs loaded with Fe²⁺, Cr²⁺ and Mn²⁺ ions at the  ωB97XD/6-31G(d,p) level of theory

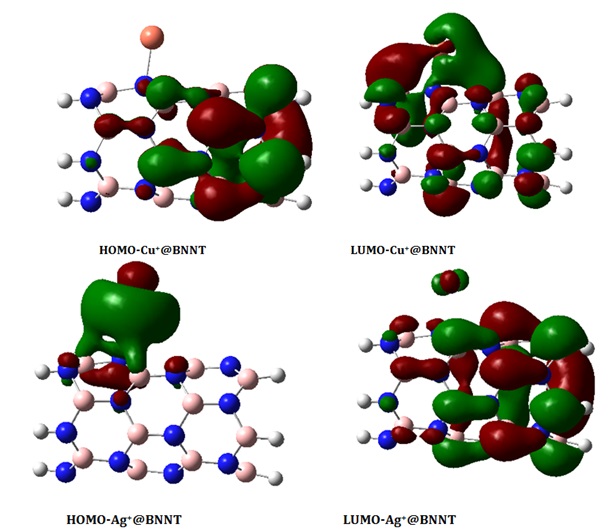
Figure 4c. Molecular orbitals of the HOMO and LUMO on the BNNTs loaded with Au⁺, Cu⁺, and Ag⁺ ions at the ωB97XD/6-31G(d,p) level of theory

Where, η represents the inherent reluctance of a chemical species to alter its electronic configuration. It is variable and might have different values within specific regions. The η value is a characteristic that pertains to molecules and not orbitals. As mentioned by the Pearson's maximum hardness principle (MHP) [45], complexes that have the lowest energy value exhibit the highest chemical hardness. The results indicate that the presence of divalent ions in the pure BNNT leads to lower η values compared to the monovalent ions, as shown in Table 3. This indicates that the previous complexes have a lower level of hardness compared to the subsequent ones. Typically, the presence of cations on free BNNTs leads to a drop in η values, which suggests an enhancement in the systems reactivity.

 In the context of an equilibrium structure, χ represents the Mulliken electronegativity of atoms and remains constant throughout the system. The electron transfer is a consequence of the disparity in electronegativity. When the cations and the BNNT engage, electron transfer occurs from the species with lower electronegativity (χ) to the species with higher electronegativity (χ). Due to the significant correlation between χ and µ (χ = -µ), electrons go towards the lower µ until the µ values become equal. To calculate the number of electrons transferred (ΔN) from the species BNNT to the cations, the quantities χ and η are utilized according to the following method [46]:

                                  (11)

The variables χ_BNNT and χ_M represent the electronegativity of the pristine BNNT and the M cations, respectively. Similarly, η_BNNT and η_M represent the chemical hardness of the pristine BNNT and the M cations, respectively. If the change in electronegativity (ΔN) is more than zero, the transfer of charge occurs from the cations to the BNNT. In this case, the BNNT acts as an electron acceptor. In contrast, if ΔN is less than zero, the charge flows from the BNNT to the cations, with the BNNT functioning as an electron donor. The ΔN values obtained from the M@BNNT complexes are negative, suggesting that the BNNT functions as an electron donor. This implies that the movement of electrons occurs from a particular filled orbital in the BNNT to a specific unoccupied orbital in the cation (see to Table 3). Therefore, according to the results, the divalent complexes exhibit a greater electron-donating ability compared to the monovalent ones.

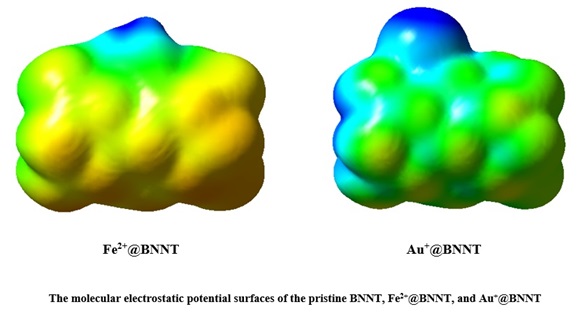
The molecular electrostatic potential (MEP) is another significant reactivity descriptor that influences the physical characteristics of the interactions inside the complexes. Figure 5 displays the MEP diagrams for the pure BNNT, Fe²⁺@BNNT, and Au⁺@BNNT. The surface of isolated BNNT exhibits blue coloration because to the presence of positively charged B atoms, while the negatively charged N atoms give it a red hue. The Au⁺@BNNT complex exhibits a considerable tendency for the electron-deficient cation to connect with the electron-rich nitrogen atom of the BNNT. This contact results in a significantly high value of E_ads, indicating a greater bond formation. The Fe²⁺@BNNT complex exhibits localized regions of negative potential on the surface of the nanotube, shown by strong red and yellow colors. However, the regions of positive potential are observed around the cation and the ring engaged in the interaction, indicated by the blue color.

Consequently, the regions with positive charge correspond to the ability of a molecule to attract nucleophiles and represent the most powerful sites of attraction. In contrast, the regions with negative charge are associated with the ability of a molecule to repel electrophiles and indicate the most powerful sites of repulsion.

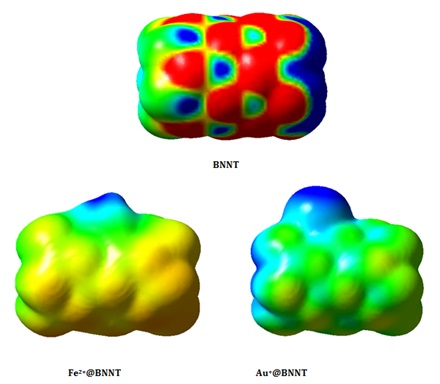
Figure 5. The molecular electrostatic potential surfaces of the pristine BNNT, Fe²⁺@BNNT, and Au⁺@BNNT

Table 4. NBO analysis of M@BNNT complexes including occupation numbers of donor (O.N._D) and acceptor (O.N._A) orbitals and their energies (E⁽²⁾, in kcal mol^-1) of some important orbitals, and the values of charge transfer (ΔQ, in e)

NBO analysis

The adsorption process involves the transfer of charge between the adsorbate and the adsorbent in both directions. Thus, the adsorbate can function as either a donor or an acceptor. Molecular polarization occurs as a result of the charge transfer that takes place during the contact process. The NBO analysis has been taken into account to assess the intermolecular interaction between species [47,48]. The findings of the analysis are reported in Table 4. The result shows a significant donor-acceptor interaction between the ions and the pristine BNNT. This interaction occurs between the bonding orbitals of the nanotube and the antibonding lone pair of cations, measured in kcal mol⁻¹ as σ_B–N →LP*_cation. In this context, the BNNT functions as the electron donor, while the ions serve as the electron acceptor.

The results demonstrate that the donor-acceptor energies (E⁽²⁾) in the complexes with divalent cations are higher than those in the complexes with monovalent cations, which aligns with the observed adsorption energies, except for the Au⁺@BNNT instance (see Table 4). Consequently, the BNNT surface exhibits a more robust affinity for divalent cations in comparison to monovalent ones. Due to the higher values of E⁽²⁾ or stronger donor-acceptor interactions of divalent cations with nanotube, these cations form more stable complexes with the BNNT surface compared to the monovalent cations. The outcome can be valuable for designing and creating novel materials that possess distinct characteristics by leveraging the interaction between cations and the surface.

Table 4 also indicates the charge transfer values (ΔQ) for the complexes under analysis. By comparing the charges of the complexed and released cations, it is simple to ascertain the charge transfer that occurs between the cations and the nanotube during complexation. The largest charge transfers take place inside the divalent cations that are adsorbed onto the BNNT, as listed in Table 4. The interaction inside the M²⁺@BNNTs is therefore stronger than that inside the M⁺@BNNTs, as confirmed by the charge transfer measurements in the complexes under analysis.

Conclusion

The present study employs the Density Functional Theory (DFT) approach to assess the adsorption of transition metal cations (Cr²⁺, Mn²⁺, Fe²⁺, Cu⁺, Ag⁺, and Au⁺) on the pristine BNNT. The adsorption of metal ions on the BNNT can be attributed to a chemisorption mechanism, which likely explains the ionic connection between the species. The adsorption energy estimated for the divalent complexes are significantly higher than those for the monovalent ones. Complexes that contain divalent cations also exhibit a greater level of reactivity compared to those having monovalent cations. During the process of adsorption, there is a transfer of electronic charge from the BNNT to the cations. The adsorption energies and donor-acceptor energies (E⁽²⁾) between the cations and the nanotube are directly related, except for the Au⁺ complex. The enhanced electrical conductivity of the BNNT due to cations adsorption suggests that this nanotube has potential for detecting specific cations. Moreover, the nanotube exhibits greater sensitivity towards divalent cations compared to monovalent cations. Furthermore, it is evident that the percentage change in E_g (%ΔE) is greater in the divalent complexes compared to the monovalent ones. Therefore, the aforementioned ions have the potential to be excellent candidates for enhanced adsorption capabilities compared to the latter scenarios. The data presented in this document can be valuable for comprehending the conduct of diverse cations on the BNNT surface and their prospective utilization in multiple domains, including catalysis, materials science, and surface chemistry. The implications of the findings on the adsorption of transition metal cations on boron nitride nanotubes for future research are significant. The structural analysis and electronic properties of transition metal cations adsorbed on boron nitride nanotubes can provide valuable insights for the development of novel applications in various fields. For instance, the unique properties of boron nitride nanotubes, such as higher thermal stability, electrical insulation, optical transparency, and neutron absorption capability, make them promising for applications in high-temperature nanocomposites, energy harvesting, electronics, and biomedicine. Therefore, the findings of the paper can potentially inspire future research endeavors aimed at leveraging the adsorption behavior of transition metal cations on boron nitride nanotubes for the advancement of nanomaterials and related technologies.

Acknowledgements

This work was supported by Vali-e-Asr University of Rafsanjan is acknowledged.

Orcid

Marziyeh Mohammadi : 0000-0003-2139-7038

Fahimeh Alirezapour : 0000-0002-2002-5884

Azadeh Khanmohammadi : 0000-0002-2444-4031

HOW TO CITE THIS ARTICLE: Marziyeh Mohammadi*, Fahimeh Alirezapour, Azadeh Khanmohammadi. Adsorption of Transition Metal Cations (Cr²⁺, Mn²⁺, Fe²⁺, Cu⁺, Ag⁺ and Au⁺) on Boron Nitride Nanotube: Structural Analysis and Electronic Properties. Adv. J. Chem. A, 2024, 7(4), 355-373.

DOI: 10.48309/ajca.2024.431676.1469

URL: https://www.ajchem-a.com/article_190505.html